16:51 Задание по математике , Поверхности второго порядка | |||||||||||||||||||||||||||
Типы поверхностей второго порядкаЦилиндрические поверхностиПоверхность S называется цилиндрической поверхностью с образующей Теорема (об уравнении цилиндрической поверхности). Кривая, задаваемая уравнением f(x,y) = 0 в плоскости z = 0, называется направляющей цилиндрической поверхности. Если направляющая цилиндрической поверхности задаётся кривой второго порядка, то такая поверхность называется цилиндрической поверхностью второго порядка.
Конические поверхностиПоверхность S называется конической поверхностью с вершиной в точке O, если для любой точки M0 этой поверхности прямая, проходящая через M0 и O, целиком принадлежит этой поверхности. Функция F(x,y,z) называется однородной порядка m, если Теорема (об уравнении конической поверхности). Если поверхность S задана функцией F(x,y,z), являющейся однородным алгебраическим многочленом второго порядка, то S называется конической поверхностью второго порядка.
Поверхности вращенияПоверхность S называется поверхностью вращения вокруг оси OZ, если для любой точки M0(x0,y0,z0) этой поверхности окружность, проходящая через эту точку в плоскости z = z0 с центром в (0,0,z0) и радиусом Теорема (об уравнении поверхности вращения).
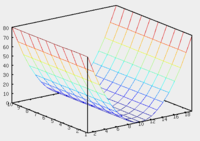
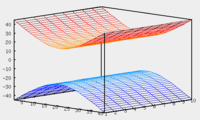
В случае, если Гиперболический параболоидВвиду геометрической схожести гиперболический параболоид часто называют «седлом». Уравнение гиперболического параболоида: При сечении гиперболического параболоида плоскостью z = z0 поверхность порождает гиперболу. При сечении гиперболического параболоида плоскостью x = x0 или y = y0 поверхность порождает параболу. Центральные поверхностиЕсли центр поверхности второго порядка существует и единственен, то его координаты
| |||||||||||||||||||||||||||
|
| |||||||||||||||||||||||||||
| Всего комментариев: 0 | |
 , если для любой точки
, если для любой точки 







 выполняется следующее:
выполняется следующее: 

 , целиком принадлежит этой поверхности.
, целиком принадлежит этой поверхности.



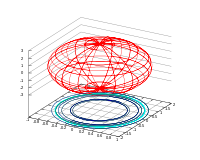



 , перечисленные выше поверхности являются поверхностями вращения.
, перечисленные выше поверхности являются поверхностями вращения.

 можно найти решив систему уравнений:
можно найти решив систему уравнений: